RAID 2 : Hamming Code ECC

      ..  RAID 2 เป็น RAID ชนิดแรกที่มีการใช้เทคโนโลยีในการตรวจจับความผิดพลาดของข้อมูล โดยอาศัยการเข้ารหัสแบบ   Hamming Code ECC(Error Checking/Correction)

ก่อนที่จะพูดถึงวิธีการเข้ารหัสแบบ Hamming Code เราไปดูการตรวจจับความผิดพลาดของข้อมูลโดยการใช้บิต Parity
กันก่อน ข้อมูลที่ถูกส่งเข้ามาเก็บในฮาร์ดดิสก์ แต่ละตัวสำหรับ RAID 2 นั้น จะมีลักษณะเป็นขบวนบิตเลขฐานสอง ซึ่งแน่นอน
ในระหว่างการส่งผ่านข้อมูล โอกาสที่ข้อมูลที่เป็นขบวนบิตนี้จะผิดพลาดที่บิตใดบิตหนึ่งย่อมเกิดขึ้นได้ จึงได้มีการคิดวิธีเติมบิต
Parity เข้าไปที่ท้ายขบวนบิตข้อมูล(1 Word) โดยบิตที่เติมเข้าไปนี้จะเป็น “0″ หรือ “1″ ก็ขึ้นกับว่าเราจะใช้การตรวจจับเป็น
แบบ Even Parity หรือ Odd Parity ลองดูตัวอย่างต่อไปนี้

..สมมติขบวนบิตที่เข้ามาเป็นดังนี้ 1 0 0 1 0 0 1 ถ้าใช้ วิธี Even Parity ในการตรวจจับความผิดพลาด บิต Parity ที่จะถูกเติมเข้าไปต่อจากขบวนบิตข้อมูลจะต้อง ทำให้ผลรวมแบบเลขฐานสองของทุกบิต (รวมบิตที่เพิ่ม เข้าไปด้วย) มีค่าเท่ากับ “0″ (วิธีจำง่ายๆ 0 + 0 = 1, 1 + 1 = 0, 0 + 1 และ 1 + 0 = 1) จากตัวอย่างผลรวม ของขบวนบิตข้อมูล (ยังไม่รวมบิต Parity ) มีค่าเป็น 1+0+0+1+0+0+1 = 1 เพราะฉะนั้นบิต Parity ที่ถูก เติมเข้าไปก็คือ “1″ เพื่อทำให้ผลรวมของทุกบิตทั้งหมด จะกลายเป็น 1 0 0 1 0 0 1 1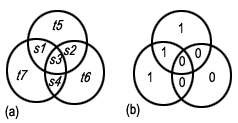

รูปที่ 3

     ..ส่วนในกรณีของ Odd Parity บิต Parity ที่จะถูกเติมเข้าไปจะต้องเข้าไปทำให้ผลรวมของทุกบิต (รวมบิต Parity ด้วย)
มีค่าเป็น “1″ และเมื่อปลายทางได้รับข้อมูลที่ผ่านการเติมบิต Parity มาแล้วก็จะสามารถตรวจสอบได้ว่าข้อมูลที่ได้รับมาผิดพลาด
หรือไม่ ยกตัวอย่างสมมติว่าเกิดผิดพลาดขึ้นที่บิตที่ 3 ทำให้ข้อมูลที่ผ่านการทำ Even Parity มาแล้วผิดพลาดเป็น 1 0 1 1 0 0
1 1 ทางฝั่งรับจะรู้ได้ทันทีว่าข้อมูลนี้ผิดพลาด โดยดูจากผลบวกของทุกบิต 1+0+1+1+0+0+1+1 = 1 ซึ่งขัดกับการทำ Even
Parity ที่ผลรวมของทุกบิตจะต้องเป็น “0″ ทางฝั่งรับก็อาจจะส่งสัญญาณตอบกลับไปที่ฝั่งส่ง ให้ทำการส่งข้อมูลมาใหม่อีกครั้ง

รูปที่ 4

… สำหรับวิธีเติมบิต Parity ที่ได้พูดไปข้างต้นนี้ ยังมีข้อเสียอยู่ตรงที่ถ้าเกิดบิตข้อมูลเกิดการผิดพลาด พร้อมกัน 2 บิต ทางฝั่งรับจะไม่สามารถตรวจจับความ ผิดพลาดได้เลยอย่างเช่นสมมติว่าบิตที่ 2 และ 3 เกิด การผิดพลาดเป็น 1 1 1 1 0 0 1 1 ผลรวมของบิตทั้ง หมดก็ยังเป็น “0″ อยู่ดี แม้จะเกิดความผิดพลาดขึ้น และข้อเสียอีกประการก็คือวิธีเติมบิต Parity นี้ ทำได้ เฉพาะตรวจจับความผิดพลาดได้เท่านั้น

     ..แต่ไม่สามารถระบุได้ว่าบิตใดเกิดความผิดพลาดขึ้น จึงทำการแก้ไขข้อมูลให้ถูกต้องไม่ได้ ด้วยเหตุนี้จึงต้องมีการคิดค้นวิธีที่จะ
เข้ามาแก้ปัญหาเหล่านี้ วิธีที่ว่าก็คือ วิธีการเข้ารหัสข้อมูล ซึ่งมีอยู่หลายวิธีด้วยกัน แต่ที่นำมาใช้ใน RAID 2 จะเป็นวิธีการเข้ารหัส
แบบ Hamming Code

     หลักการของการเข้ารหัสก็คือ ขบวนบิตข้อมูลจำนวน k บิต จะถูกเข้ารหัสให้กลายเป็นคำรหัส (Code Word) ที่มีความยาว
  n บิต โดยจะมีการเติมบิตที่ใช้ในการตรวจสอบ (Check Bits) n - k บิตต่อท้ายบิตข้อมูล โดยบิตที่ใช้ในการตรวจสอบนี้จะมี
ความสัมพันธ์กับบิตข้อมูลด้วย ส่วนจะสัมพันธ์ในรูปแบบไหนก็ขึ้นอยู่กับว่าใช้การเข้ารหัสแบบใด ในส่วนของการเข้ารหัสแบบ
Hamming Code นี้จะอาศัยการสร้างบิตตรวจสอบจากวิธีการดังนี้

    ในการเข้ารหัสแบบ Hamming Code จะใช้ขบวนบิตข่าวสาร 4 บิต และจะมีการเติมบิตที่ใช้ในการตรวจสอบเข้าไป 3 บิต
รวมเป็น 7 บิต สมมติให้ s1 - s4 แทนขบวนบิตข้อมูล และ t5-t7 แทนบิตตรวจสอบ ดังนั้นขบวนบิตทั้งหมดหลังจากการทำการ
เข้ารหัสแล้วจะเป็นดังนี้ s1-s2-s3-s4-t5-t6-t7 บิต t5-t7 หาได้จากวิธีในรูปที่ 3

s	t	s	t	s	t	s	t
0000	0000000	0100	0100110	1000	1000101	1100	1100011
0001	0001011	0101	0101101	1001	1001110	1101	1101000
0010	0010111	0110	0110001	1010	1010010	1110	1110100
0011	0011100	0111	0111010	1011	1011001	1111	1111111

      ..หลักการหาก็คือว่าทั้ง t5, t6 และt7 จะต้องมีค่าที่ทำให้ผลรวมของบิตในแต่ละวงกลมเป็น Even(”0″) อย่างตัวอย่างใน
รูปที่ 3-b ถ้า s = 1 0 0 0 บิต t5 ก็ต้องเป็นบิตที่ทำให้ผลรวมของ s1-s2-s3-t5 เป็น “0″ ดังนั้น t5 จึงเป็นบิต “1″ ก็ทำใน
ลักษณะเดียวกัน ดังนั้นขบวนบิตหลังจากผ่านการเข้ารหัสก็จะเป็น 1 0 0 0 1 0 1 ตารางที่ 1 แสดงขบวนบิตข้อมูลที่เป็นไป
ได้ทั้งหมดกับขบวนบิตหลังผ่านการเข้ารหัส

       ..สำหรับการเข้ารหัสโดยวิธี Hammimg Code นี้ จะได้เปรียบวิธีเติมบิต Parity ตรงที่ทางฝั่งรับสามารถระบุได้ว่าบิต
ใดเกิดความผิดพลาดขึ้น จึงทำให้เราสามารถแก้ไขความผิดพลาดที่เกิดขึ้นได้ แต่มีข้อแม้ว่าข้อผิดพลาดนั้นต้องมีเพียงบิตเดียว และต้องไม่ใช่บิต s3 ลองพิจารณาดูรูปที่ 4 สมมติว่าใช้ขบวนบิตที่ผ่านการเข้ารหัสมาแล้วเหมือนตัวอย่างที่แล้วคือ 1 0 0 0 1
0 1 แล้วเกิดความผิดพลาดที่บิต s2 ทำให้ข้อมูลเปลี่ยนเป็น 1 0 1 0 1 0 1 หรือเขียนเป็นไดอะแกรมได้ตามรูปที่ 4a จะเห็นได้
ว่าจะมีเฉพาะวงกลมเส้นประเท่านั้นไม่เป็นไปตาม Even Parity ดังนั้นบิตที่เป็นไปได้ที่จะทำให้เกิดความผิดพลาดกับวงกลม
ทั้งสองวงก็คือบิต s3 = 0 และ s2 = 1 แต่เราจะตัดการพิจารณาบิต s3 ออกไปเพราะบิต s3 อยู่ในอาณาเขตของวงกลมเส้น
ทึบด้วย สาเหตุก็เนื่องมาจากว่าถ้าบิต s3 เกิดความผิดพลาด มันก็จะไปส่งผลกระทบต่อ Even Parity ของวงกลมเส้นทึบด้วย
จึงเหลือบิตให้พิจารณาเพียงบิตเดียวคือ s2 เพราะฉะนั้นทางฝั่งรับก็จะรู้ได้ทันทีว่าบิต s2 เป็นบิตผิดพลาด ก็จะมีการแก้ไขเกิด
ขึ้นโดยการกลับบิตจาก “1″ เป็น “0″ ส่วนรูปที่ 4b บิตที่ผิดพลาดจะเป็นบิต t5 ซึ่งเป็นการตรวจสอบที่เพิ่มเข้าไป จากรูปจะเห็น
ได้ว่า ถ้าบิตตรวจสอบเกิดความผิดพลาด ทางฝั่งรับจะรู้ได้ทันทีว่าเป็นบิตไหน เพราะวงกลมเส้นประจะเกิดขึ้นแค่วงเดียว และ
บิต s1, s2 และ s3 ก็อยู่ในอาณาเขตของวงกลมทึบด้วย ดังนั้นจึงมีเพียงบิตเดียวที่อยู่ในวงกลมเส้นประล้วนๆนั้นคือบิต t5
ในรูปที่ 4c จะเป็นไดอะแกรมแสดงจุดบอดของวิธี Hamming Code เพราะถ้าบิตตรงกลางวงกลม บิต s3 เกิดผิดพลาดขึ้น
ทางฝั่งรับจะไม่มีทางรู้ได้เลยว่าบิตใดผิดพลาด เพราะวงกลมทั้งสามวงเป็นเส้นประหมด โดยทางฝั่งรับจะตีความว่าข้อมูล
ที่ได้รับเกิดการผิดพลาด แต่จะไม่มีการแก้ไขใดๆ เกิดขึ้นต้องให้ทางฝั่งส่ง ทำการส่งข้อมูลมาใหม่เท่านั้น






     ..ทางฝั่งรับข้อมูลจะมีตารางข้อมูลแบบตารางที่ 1 เอาไว้เพื่อถอดรหัสเอาข้อมูลออกมา เช่นเดียวกับทางฝั่งส่ง ใน RAID 2 นั้น
ฮาร์ดดิสก์แต่ละตัวจะเก็บข้อมูลที่เข้ามาทีละบิตๆ ดูรูปที่ 5 A0-A3 จะแทนข้อมูล 1 word โดยทั้ง 4 บิตนี้จะผ่านการเข้ารหัสแบบ
Hamming Code โดยการเติมบิตตรวจสอบ ECC/Ax, ECC/Ay และ ECC/Az เข้าไป ทำให้ RAID 2 มีความสามารถ
ในการแก้ไขความผิดพลาดได้ แต่ข้อเสียที่เราเห็นได้อย่างชัดเจนของ RAID 2 ก็คือการที่มันต้องใช้ฮาร์ดดิสก์ เพื่อเก็บบิตตรวจ
สอบเกือบๆเท่ากับจำนวนฮาร์ดดิสก์ที่ใช้เก็บข้อมูล เพราะยิ่งขนาด word ของข้อมูลเล็กเท่าไหร่สัดส่วนระหว่างฮาร์ดดิสก์ทั้งสอง
ชนิดก็ยิ่งเกือบจะเท่าๆกัน ดูจากรูปที่ 5 นั่นก็หมายความว่า เราต้องเสียค่าใช้จ่ายอีกประมาณเกือบเท่าตัวในการเก็บบิตตรวจสอบ
ซึ่งเป็นเรื่องที่ค่อนข้างสิ้นเปลืองทีเดียว

---